[딥러닝] Deep learning (딥러닝)
- -
딥러닝의 기본 개념부터 알아봅시다.
신경망(Neural Network)
인간 두뇌에 대한 계산적 모델을 통해 인공지능을 구현하려는 분야. 신경세포 뉴런(neuron)의 이름을 따왔다.
이 뉴런을 흉내내어 만든 신경망 모델을 퍼셉트론(Perceptron)이라고 한다.
퍼셉트론(Perceptron)
로젠블랏이 제안한 학습 가능한 신경망 모델. 입력변수를 받아 선형 결합한 후 비선형으로 전환하여 결과를 도출한다.

다층 퍼셉트론(Multi-layer Perceptron; MLP)
여러 개의 퍼셉트론을 층 구조로 구성한 신경망 모델

| 입력층(Input layer) | 은닉층(Hidden layer) | 출력층(Output layer) |
| 입력변수의 값이 들어오는 곳 | 다수 노드 포함 가능 | (범주형이면) 출력 노드의 수 =출력변수의 범주 개수 |
| 입력변수의 수 = 입력노드의 수 | 다수의 은닉층 형성 가능 | (연속형이면) 출력 노드의 수 = 출력변수의 개수 |
Neural Network의 파라미터: 층 간 노드를 결정하는 가중치들 (알고리즘으로 결졍)
Neural Network의 하이퍼파라미터: 은닉층 개수, 은닉노드 개수, 활성화 함수 등 (사용자가 임의로 결졍)
활성화 함수 (Activate Function)
아래 여섯 개 종류의 활성화 함수가 있다.

비용함수
뉴럴네트워크 모델로붙터 나온 Y값과 실제 Y값의 차이를 최소로 하는 가중치
이 비용함수를 최소화하는 파라미터를 찾는 것이 목표가 된다.
$$argmin_w \sum_{i} L(Y, f(X;w))$$
분류에서는 아래와 같은 cross entropy를 사용한다. $$L=-\sum_i t_i logp_i \; \; (단, \; 미분가능해야 \; 한다)$$
$$C(y_i, \hat{y_i})=\left\{\begin{matrix}
-log \,\hat{y_i}, \;\;\;\;\;\;\;\;\;\;\;\; y=1 \\ -log(1-\hat{y_i}), \;\;\; y=0
\end{matrix}\right.$$
예측값과 실제값의 차이를 측정하는 방법으로 MSE를 사용한다. $$L=\frac{1}{2}(o-t)^2 \; \; (o: 예측값 \; t: 실제값)$$
즉 뉴럴네트워크에서는 $L(Y,\hat{Y})=\sum_{i=1}^{N}\left\{ -y^{(i)} \cdot log(\hat{y}^{(i)})-(1-y^(i))\cdot log(\hat{y}^{(i)}) \right\}$를 이용하여 예측값과 실제값의 차이를 계산한다.
뉴럴 네트워크 학습은 경사하강법을 사용한다. 경사하강법에 대한 설명은 이전 포스트를 참고하자.
[데이터마이닝] 선형회귀분석
들어가기 전 기계학습의 진짜진짜 간단한 구성 요소부터 알아봅시다 알고 있다면 넘겨도 무관 더보기 Input x (in 다변량 데이터, 독립변수/예측변수/입력변수...) Output y (in 다변량 데이터, 종속변
bubble2.tistory.com
역전파 알고리즘
MLP를 학습시키기 위한 방법. 연쇄법칙에 기반한다.
순전파는 입력층→출력층, 역전파는 출력층→입력층 방향으로 계산하면서 가중치 w를 업데이트한다.
Softmax function
다중 클래스 분류 모델을 만들 때 사용하는, 이진 분류를 수행하는 활성화 함수이다. Output layer의 크기를 범주 개수만큼 설정하고 softmax를 이용하면 다중 범주 분류 모델로 쉽게 변형 가능하다. $$p(y=i | x) = s_i = \frac{e^{z_i}}{\sum_{j} e^{z_j}}, \;\; i=1,2,...,C$$
Batch size: 1회 트레이닝에 사용할 관측치의 수. 클수록 빠르지만 성능이 저하되고, 작을수록 느리지만 확실한 성능을 보인다.
Epochs: 전체 데이터에 대해 학습을 반복하는 횟수.
Early stopping: 오버피팅을 방지하기 위해 학습 과정을 모니터링하여 조기에 학습을 종료하는 것.
Deep Neural Network (DNN, 심층 신경망)
여러 층으로 이루어진 복잡한 구조의 인공신경망. 2006년 이전에는 2개 이상의 층을 학습하는 것이 거의 불가능했지만 Geoffrey Hinton에 의해 많은 층을 학습할 수 있게 되었다. DNN은 고차원의 raw data(음성, 이미지, 텍스트 등)를 그대로 사용해도 자동으로 속성(feature)를 정의할 수 있으며 기존의 기계학습 방법론에 비해 예측 정확도가 우수하다. 또한 특정 데이터(도메인)에서 학습된 구조를 다른 데이터(도메인)에서도 사용할 수 있는 전이학습이 가능하다.
과거에 층을 많이 사용할수록 학습이 안 되는 이유는 Vanishing gradient problem 때문이었다. 이는 Sigmoid 활성화 함수를 사용할 경우 은닉층의 수가 증가함에 따라 하위 층으로 갈수록 gradient가 0이 될 가능성이 높아져 오류 역전파가 잘 수행되지 않았다. 즉 입력층에 큰 범위를 가지는 실수를 넣어도 출력층에는 작은 변화로 기록되었다.
▶ 이를 해결하기 위해 gradient가 소실되지 않은 새로운 활성 함수를 사용한다. 이 함수가 바로 Rectified Linear Unit(ReLU) 함수이다. 이 함수는 입력이 0보다 작을 때는 0을, 0보다 큰 값에 대해서는 해당 값을 그대로 사용하는 $max(0,x)$ 함수이다.
또한 층을 많이 사용하면 과적합이 발생하는 문제점도 있었다. 은닉층과 은닉 노드의 수가 증가하면 특정 형태의 함수나 분류 경계를 찾아낼 가능성이 있었다. 데이터의 숫자가 적을 때는 이러한 특징이 꼭 좋은 게 아니기 때문에 문제점으로 지적했다. 이를 해결하기 위해 두 가지 관점에서의 해결 방안을 제시한다.
▶ 모델 관점에서의 Drop-Out
학습 과정에서 일부러 특정 노드들에 연결된 가중치들의 업데이트를 하지 않는 방법이다. 업데이트를 하지 않을 노드는 무작위로 설정한다.
▶ 데이터 관점에서의 Data Augmentation
사용하고 싶은 모델의 파라미터 수가 많은데 데이터의 수가 적으면 과적합이 발생할 수 있다. 이 경우 현재 보유한 데이터를 증폭해서 과적합도 막고 모델 정확도도 향상시킬 수 있다. 이미지 사진을 예로 들면, 하나의 사진을 자르기, 회전, 반전, 뒤집기, 회색조 등의 방법으로 데이터 양을 늘릴 수 있다.
Convolutional Neural Network (CNN, 합성곱 신경망)
시각적 이미지 분석에 가장 일반적으로 사용되는 인공신경망의 한 종류로, 입력 이미지로부터 특징을 추출하여 입력 이미지가 어떤 이미지인지 클래스를 분류하는 인공싱경망이다. 이미지와 비디오 인식, 추천 시스템, 이미지 분류, 의료 이미지 분석 및 자연어 처리에 응용된다. CNN에 사용되는 이미지에 대해 알아보자.
흑백 이미지는 2차원의 행렬로 표현되며 행렬은 흑백의 톤을 실수 값으로 표현한다. 반면 컬러 이미지는 3차원의 텐서(Tensor)로 표현된다. RGB(Red, Green, Blue) 각각의 행렬은 색의 톤을 실수 값으로 표현한다. 그러나 이 각각의 픽셀을 하나의 변수로 간주하여 모델링하면 Input layer와 Output layer 사이에 너무 많은 가중치가 생겨 학습이 어려워진다. 따라서 변수의 수를 줄이기 위해 Low level 변수를 조합하여 보다 적은 수의 변수를 생성하게 된다.
이미지의 경우 인접 변수(픽셀)간 높은 상관관계를 가지므로 이를 고려하기 위해 spare connection을 구성, 즉 인접한 변수만을 이용하여 새로운 feature를 생성한다.
또한 이미지의 부분적 특성(눈, 귀 등)은 고정된 위치에 등장하지 않는다. 이를 추출하기 위해 인접한 변수 집합에 동일한 가중치를 적용하는 shared weight를 이용한다.
☞이 둘을 실현시킨 방법을 convolution이라고 한다.
합성곱 연산
합성곱 계층에서의 합성곱 연산은 이미지처리에서 말하는 필터(마스크)연산에 해당한다. 2차원의 입력 데이터가 들어오면 필터(커널)의 윈도우가 일정 간격으로 이동해가며 연산이 적용된다. 이 과정을 모든 부분에 적용하면 합성곱 연산의 출력이 완성되는 것이다.

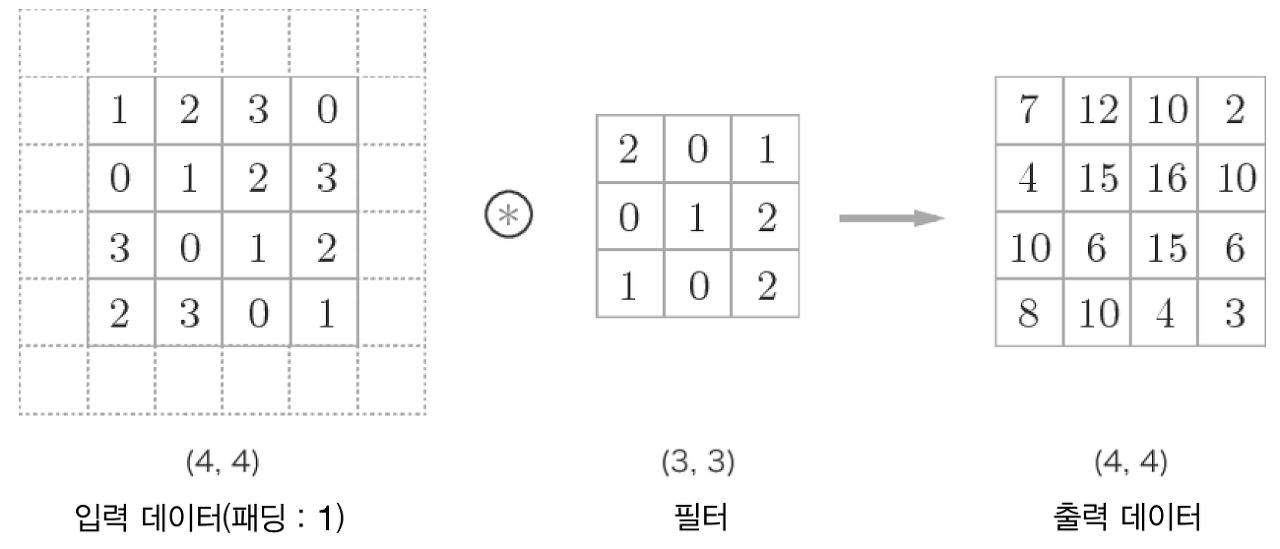
패딩 (Padding) 처리란...
입력 데이터와 출력 데이터의 크기를 맞추기 위해 사용된다. 위에서 본 것처럼 합성곱 연산 수행 시 데이터의 크기가 줄어드는데, 연산 수행 전 입력 데이터 주변(가장자리)을 특정 값으로 채우는 것을 말한다. 이때 주로 0을 사용한다.
가장자리에 있는 픽셀들은 중앙에 위치한 픽셀들에 비해 Convolution 연산이 적게 수행된다. 이를 위한 해결책으로 원 이미지 테두리에 0의 값을 갖는 픽셀을 추가하는 것이다.
스트라이드(Stride)란...
필터를 적용하는 위치의 간격을 말한다. 스트라이드가 커지면 출력 크기가 작아진다.
출력 크기 $(OH, OW)$는 원소의 개수를 의미하므로 정수로 나누어 떨어지는 값이어야 한다. 딥러닝에서 값이 딱 나누어 떨어지지 않을 때 반올림하여 가장 가까운 정수로 만들기도 한다. $$OH = \frac{H+2P+FH}{S}+1$$ $$OW=\frac{W+2P+FW}{S}+1$$
입력 크기: $(H,W)$
필터 크기: $(FH, FW)$
출력 크기: $(OH, OW)$
패딩: $P$
스트라이드: $S$

채널을 가진 3차원 데이터의 합성곱 연산은 채널마다 합성곱 연산을 수행한 뒤 그 결과를 더해서 하나의 결과를 얻는 방법으로 진행된다.

풀링(Pooling) 연산이란...
세로와 가로 방향의 공간을 줄이는 연산으로, 일정 영역의 정보를 축약하여 크기를 줄인다. 풀링의 윈도우 크기와 스트라이드 값을 같게 하는 게 일반적이다. 풀링 시 패딩은 보통 사용하지 않는다.
최대 풀링: 대상 영역에서 최댓값을 취하는 방법. 이미지 분석에서 주로 사용한다.
평균 풀링: 대상 영역의 평균을 취하는 방법.
완전 연결층이란...
위와 같이 추출된 특징 값을 기존 뉴럴 네트워크에 넣어서 이미지를 분류한다. 이때 뉴럴 네트워크에 특징들을 전달하기 위해 행렬을 1차원 자료로 변환하는 Flattening 작업이 필요하다.
합성곱 신경망 (CNN) 구조
기존의 신경망 구조는 인접하는 계층의 모든 뉴런이 완전 연결(fully-connected)로 결합된 형태로, Affine 계층으로 구성된다.

반면 합성곱 신경망 구조는 신경망 구조에서 합성곱 계층과 풀링 계층이 추가된 형태이다.

CNN의 하이퍼파라미터
필터 크기: 필터의 크기와 모양
필터 수: 얼마나 다양한 정보를 추출한 것인지 결정 (많을수록 다양성 증가)
스트라이드: 필터가 건너뛰는 픽셀 수 (클수록 띄엄띄엄 이동)
제로 패딩: 합성곱 연산의 편의성을 위해 사용 (위 하이퍼파라미터에 따라 결정)
'Data theory > 딥러닝' 카테고리의 다른 글
| [논문 요약/정리] 뇌졸중 데이터를 통한 머신러닝, 딥러닝 예측 및 분류 기법 성능비교 (1) | 2024.11.27 |
|---|---|
| [딥러닝] 서포트 벡터 머신 (SVM) (0) | 2023.10.15 |
| [딥러닝] KNN (0) | 2023.10.15 |
| [딥러닝] 군집 분석 (Clustering) (0) | 2023.10.14 |
소중한 공감 감사합니다